One of the first questions that comes up when we start working with Abaqus is:
What units shall I use for the density, elastic modulus or even the dimensions of my model? I mean, what units should I use for the length, time, mass, force, stress or any other magnitude?
Actually, the answer to this questions is not unique… But before giving an answer, I would like to briefly introduce magnitudes and units.
1. Types of magnitudes
Before going on, let’s remember that there are: fundamental magnitudes and derivate magnitudes
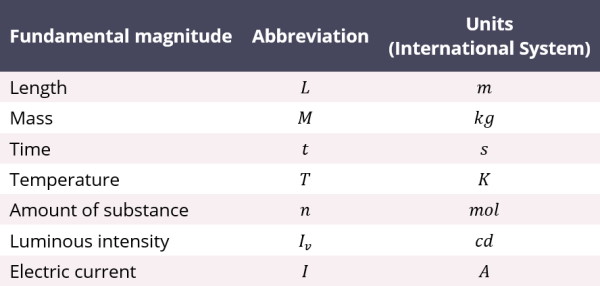
There are 7 fundamental magnitudes from which we can define any other magnitude. They are summarized in the following table:
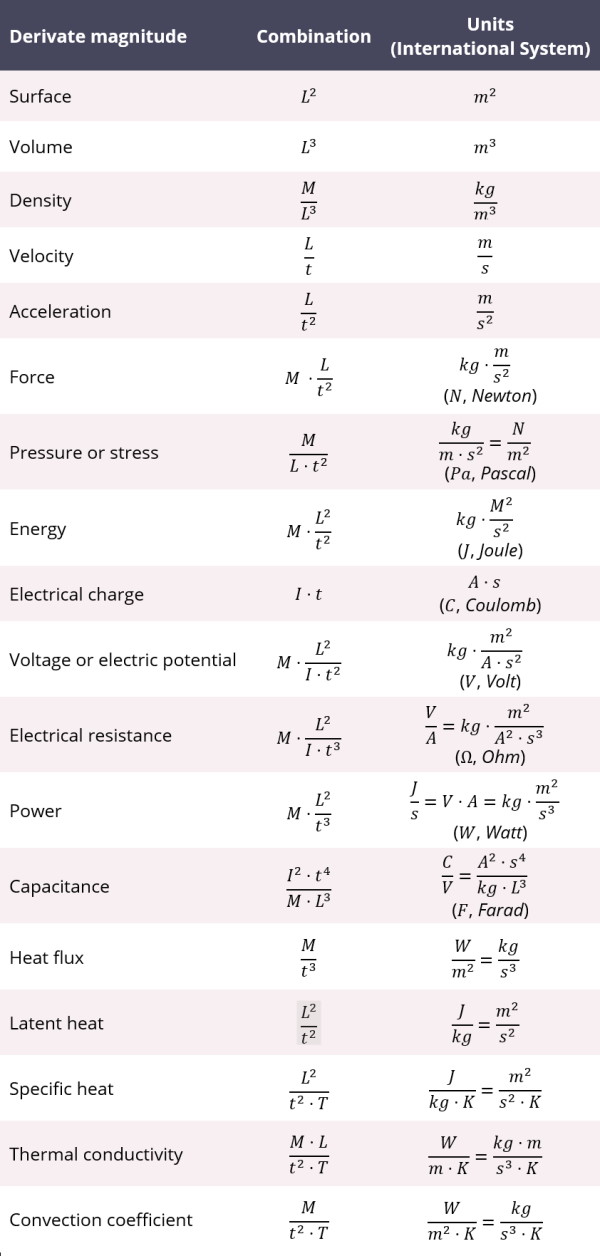
Derivate magnitudes are defined by combining fundamental magnitudes. Although there is a huge number of derivate magnitudes, some of the most common in mechanical, electrical and thermal disciplines are the following:
2. The units system of Abaqus
The first thing we need to know is that Abaqus does not oblige to use any particular units system, such as the International System or the Imperial System. Instead, it follows a coherent units system. What does it mean?
Let’s say that we have sketched our part using meters for the length (m). It involves that every derivate magnitude based on length (L), will take it in meters. In this way, we could introduce the rest of magnitudes in units of the International System (SIU), so for a material as steel we would end up like:
$$\begin{align*}
\rm{Elastic\ modulus} &: E=210 \cdot 10^9\,\rm{(Pa)} \\
\rm{Poisson\ ratio}&: \nu=0.3\, \rm{(non\, dimensional)} \\
\rm{Density} &: \rho=7800\,\rm{(kg/m^3)}
\end{align*}$$
3. Alternative units systems
However, if we do that, we will be working with huge quantities. Especially when dealing with stresses, which are in the order of MPa (millions of pascals).
To avoid that, we can take advantage of the coherent units system of Abaqus and make a smart choice of the fundamental magnitudes for our model. Some of the most convenient units systems in mechanics, depending on the model size, are shown in the table below:
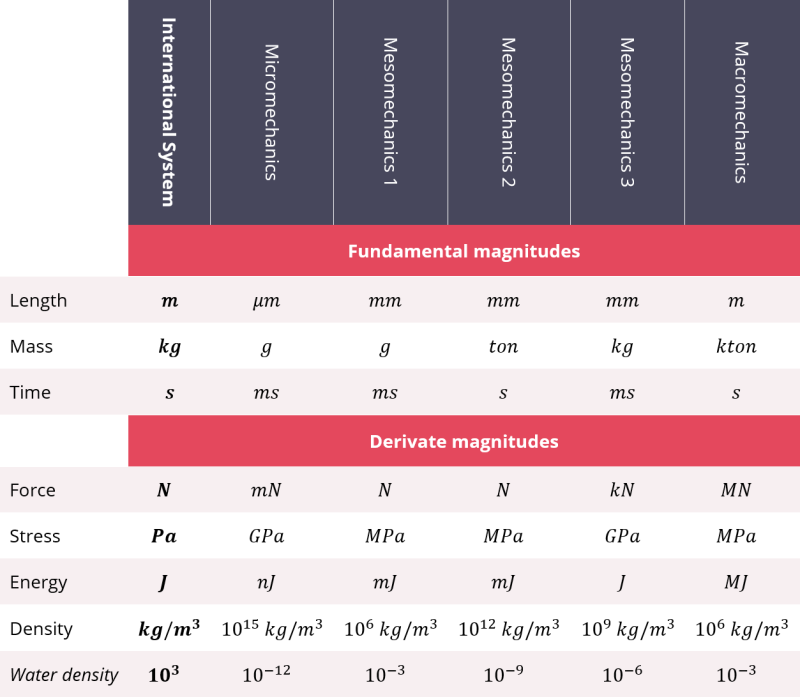
My favourite units system is the one I called ‘Mesomechanics 2‘, because it combines length in millimeters (mm), time in seconds (s) and stress in megapascals (MPa). Hence, for the material shown before:
$$\begin{align*}
\rm{Elastic\ modulus} &: E=210 \cdot 10^3\,\rm{(MPa)} \\
\rm{Poisson\ ratio}&: \nu=0.3\, \rm{(non\, dimensional)} \\
\rm{Density} &: \rho = 7.8 \cdot 10^{-9}\,(10^{12}~\rm{kg/m^3})
\end{align*}$$
There are very small models devoted to analyzing microscopic phenomena, also known as Computational Micromechanics (CMM). In these cases, it is much more convenient to use microns for the length (μm). The best suited units system for CMM models is the one named “Micromechanics”, with stresses in GPa.
On the other hand, if the model expands along dozens or hundreds of meters, as it occurs in big infrastructures (e.g. bridges, skyscrapers, wind turbines…). It is preferred to use meters for the length (m). Adopting the “Macromechanics” system seems to be the most appropriate taking the mass in kilotons (1 kton = 1000 ton) and time in seconds. You can check that, like this, stress will be in MPa.
4. Practical usage of units systems
In the next video I will show you how to use different units systems in Abaqus. In addition, you will find some tips to improve the visualization of your results.
5. What next?
Do you want to know how to simulate an impact or import external geometry in Abaqus and take advantage of Python scripts to automate all the process? Then, you can take a look at this blog post
I hope you learned something and see you in the next one!



